Neuron Model

This document details the spiking neuron model used in Axon, which implements the STICK computation framework. STICK uses temporal coding, precise spike timing, and synaptic diversity for symbolic and deterministic computation.

STICK: Spike Time Interval Computational Kernel, A Framework for General Purpose Computation using Neurons, Precise Timing, Delays, and Synchrony.

Overview

Axon simulates event-driven, integrate-and-fire neurons with:

Millisecond-precision spike timing
Multiple synapse types with distinct temporal effects
Explicit gating to modulate temporal dynamics

The base classes are:

AbstractNeuron: defines core membrane equations
ExplicitNeuron: tracks spike times and enables connectivity
Synapse: defines delayed, typed connections between neurons

Neuron Dynamics

Axon simulates event-driven non-leaky integrate-and-fire neurons.

The membrane potentail (V) evolves following the differential equations:

\[ \tau_m \frac{dV}{dt} = g_e + \text{gate} \cdot g_f \] \[ \frac{dg_e}{dt} = 0 \] \[ \tau_f \frac{dg_f}{dt} = -g_f \]

Each neuron has 4 internal state variables:

Variable	Description
`V`	Membrane potential
`ge`	Constant input
`gf`	Exponential input
`gate`	Binary gate controlling `gf`

Each neuron also has 4 internal parameters:

Parameter	Description
`Vt`	Membrane potential threshold
`Vreset`	Membrane potential set after a reset
`tm`	Timescale of the evolution of the membrane potential
`tf`	Timescale of the evolution of `gf`

When the membrane potential surpasess a threshold, V > Vt, the neuron emits a spike and resets:

if V > Vt:
    spike → 1
    V → Vreset
    ge → 0
    gf → 0
    gate → 0

Neuron Model Animation

This animation demonstrates the evolution of an individual neuron under different synaptic inputs (V, ge, gf, gate):

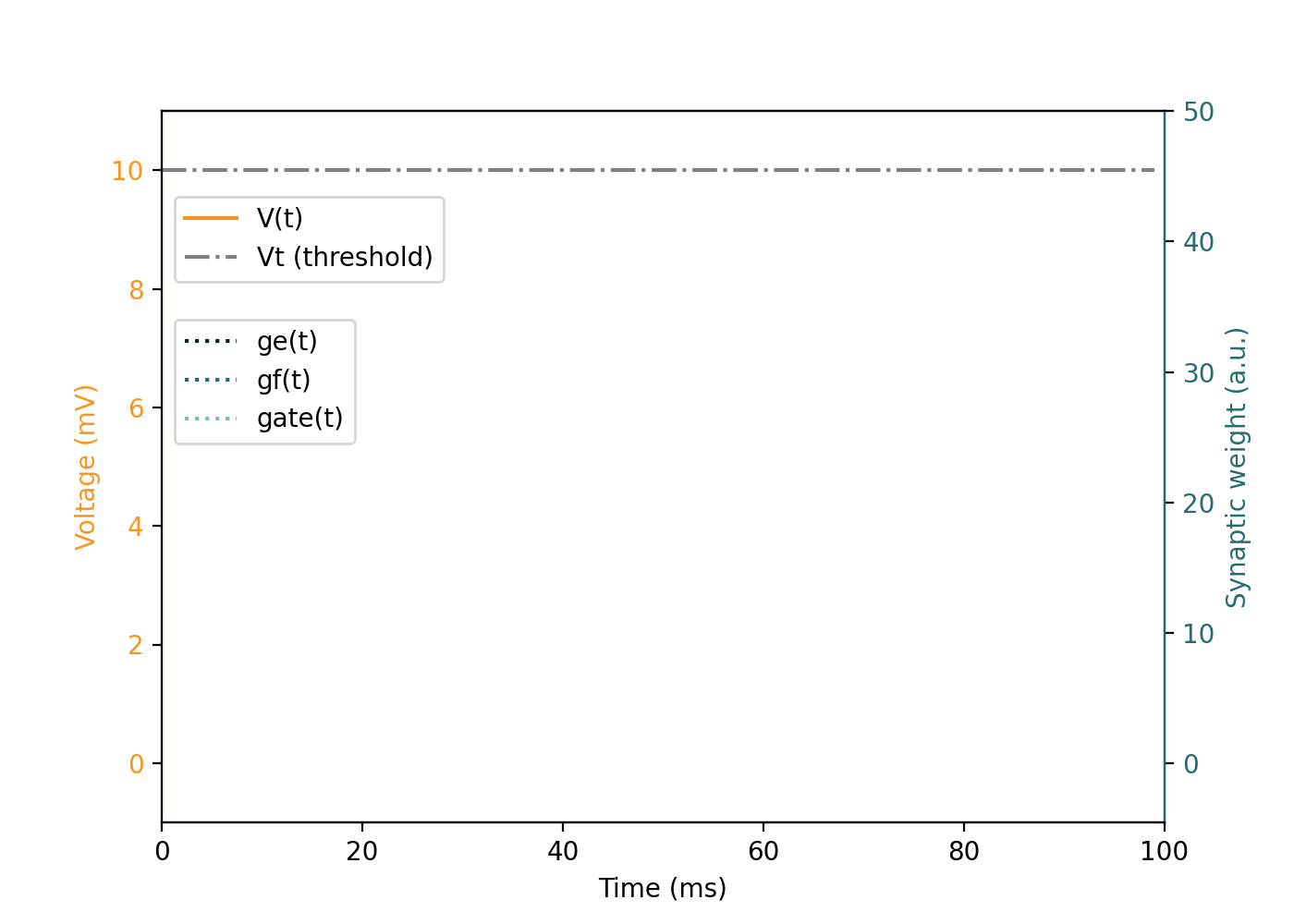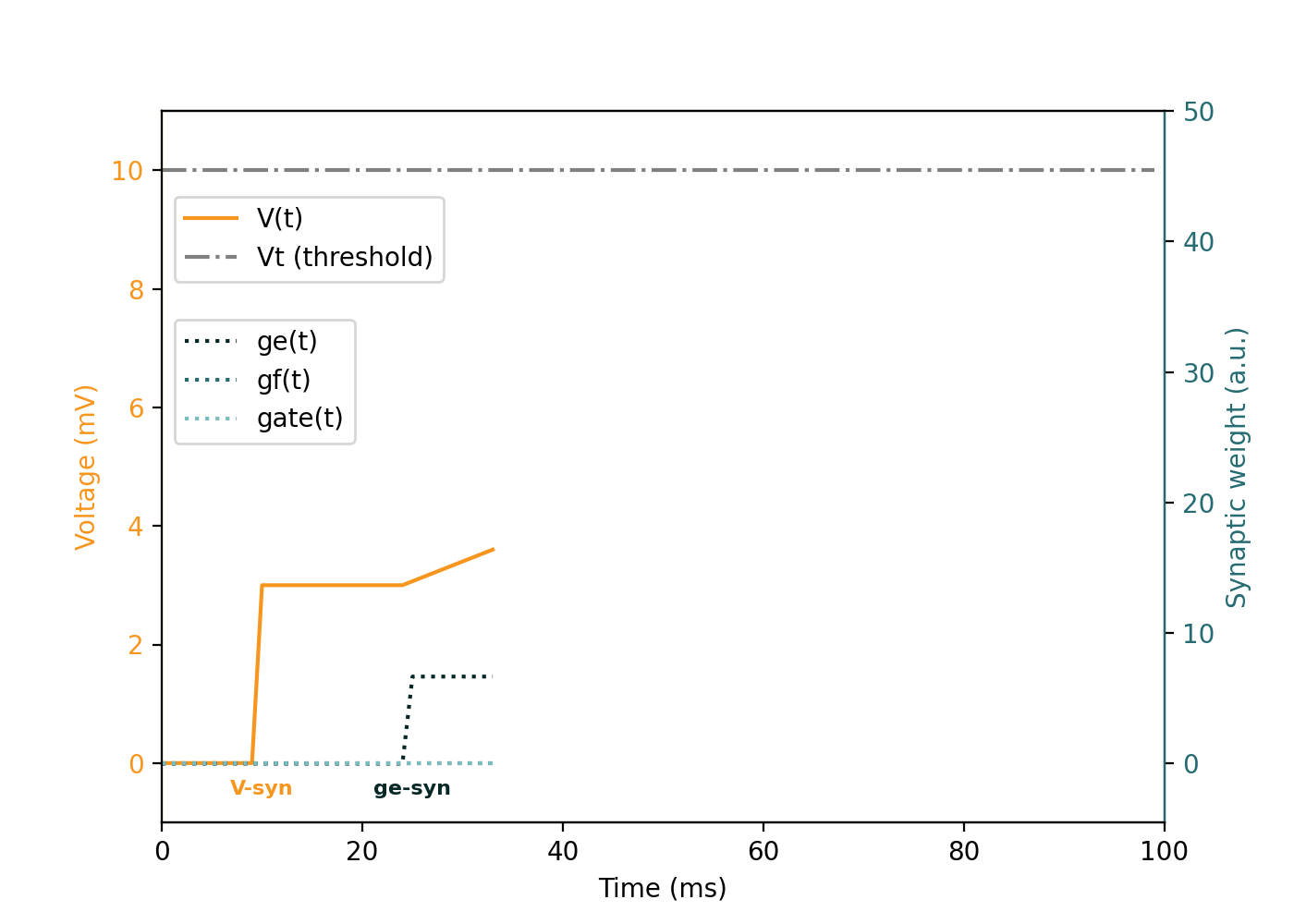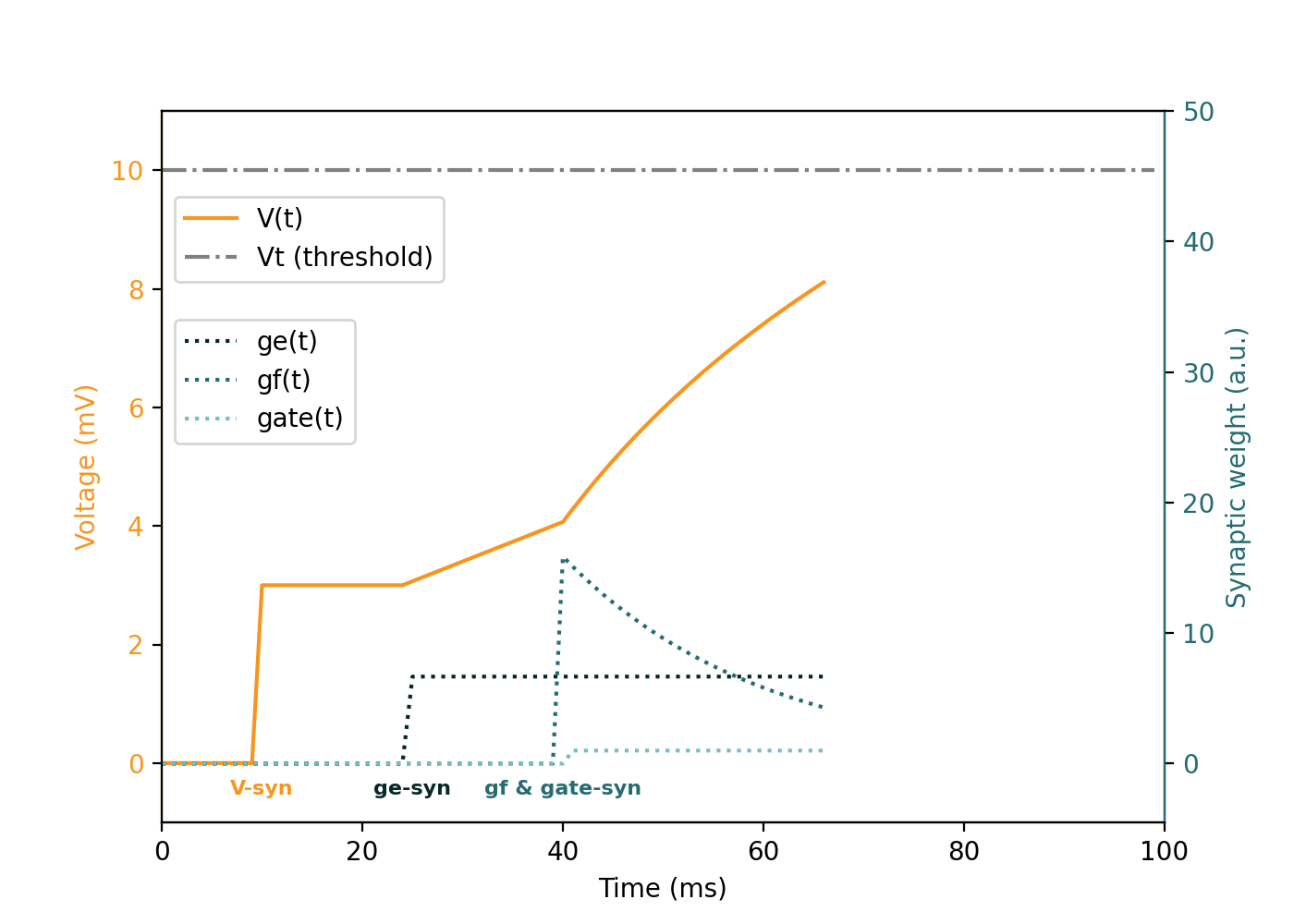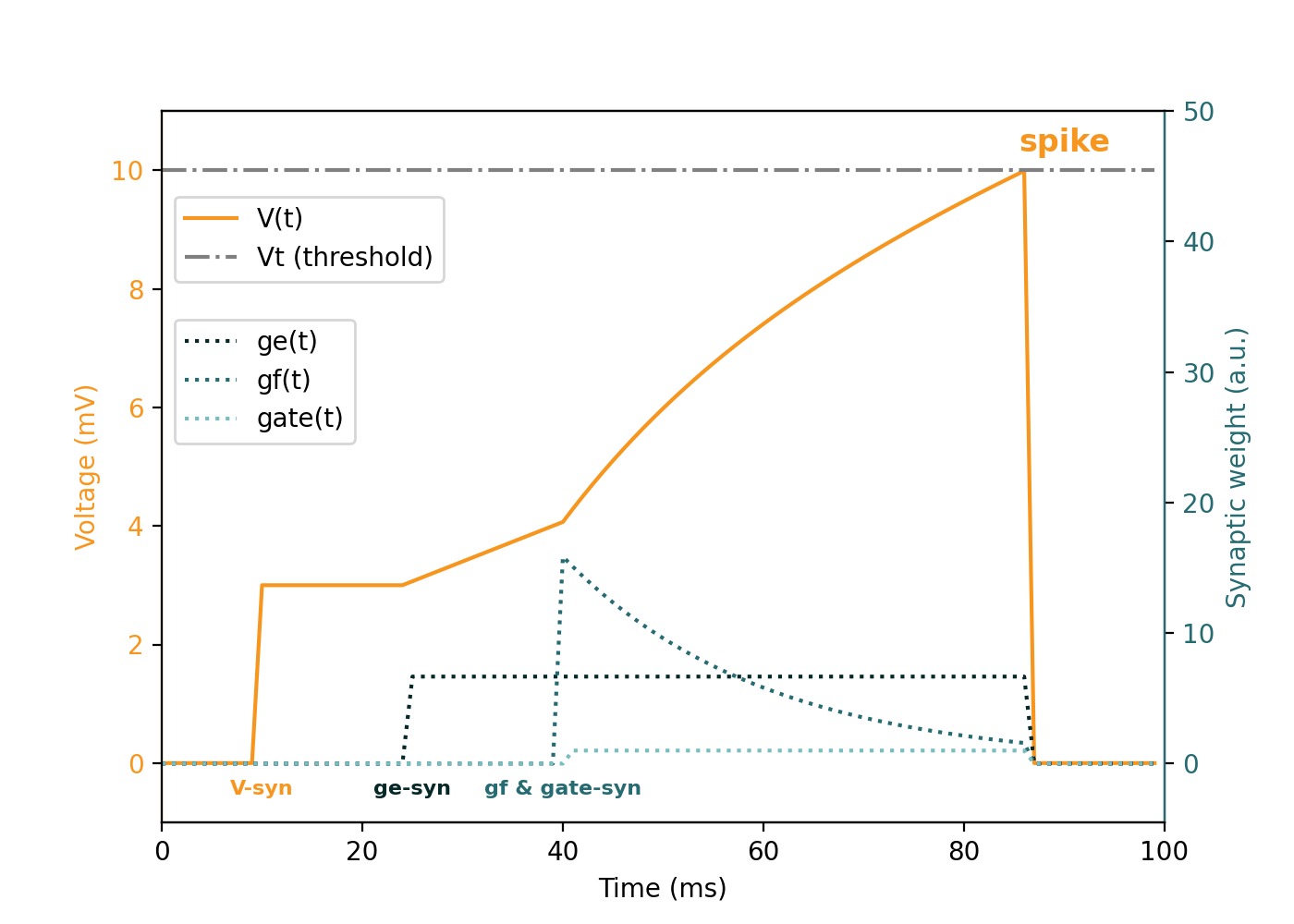
Neuron

Synapse Type	Behavior
`V`	Instantaneous jump in membrane potential `V`, potentially emitting spike
`ge`	Slow, steady increase in `V` over time
`gf + gate`	Fast, nonlinear voltage rise due to exponential dynamics
`gate`	Controls whether `gf` affects the neuron at all

Event-by-event explanation of the animation

Time (ms)	Type	Value	Description
`t = 10`	`V`	3.0	Instantaneous pushes of `V`, membrane potential
`t = 25`	`ge`	6.0	Applies constant integration current: slow, linear voltage increase
`t = 40`	`gf`	16.0	Adds fast-decaying input, gated via `gate = 1` at same time
`t = 40`	`gate`	1.0	Enables `gf` affecting neuron dynamics
`t = 85`	`spike`	-	Neuron emits a spike and resets its state

Synapse Types

The neuron model has 4 synapse types. Each of them affects one of the 4 internal state variables of the neuron receiving the synapse. Synapses have a certain weight (w):

Synapse Type	Effect	Explanation
`V`	`V += w`	Immediate change in membrane potential
`ge`	`ge += w`	Adds to the constant input
`gf`	`gf += w`	Adds to the exponential input
`gate`	`gate += w`	Toggles gate flag (`w = ±1`) to activate `gf`

Besides it’s weight w, wach synapse also includes a delay, controlling the the time taken by a spike travelling through the synapse to arrive to the following neuron and affecting it’s internal state:

synapse
  | weight
  | delay

Numerical Parameters

By default, Axon uses the following numeric values for the neuron parameters

Parameter	Numeric value (mV, ms)	Meaning
`Vt`	10.0	Spiking threshold
`Vreset`	0.0	Voltage after reset
`tm`	100.0	Membrane integration constant
`tf`	20.0	Fast synaptic decay constant

Units are milliseconds for time values and millivolts for membrane potential values.

Benefits of This Model

This neuron model is designed for interval-coded values. Time intervals between spikes directly encode numeric values.

The neuron model has dynamic behaviours that eenable symbolic operations such as memory, arithmetic, and differential equation solving. The dynamics of this neuron model forms a Turing-complete computation framework (for in depth information, refer to the STICK paper).

This neuron model has the following characteristics:

Compact: Minimal neurons required for functional blocks
Precise: Accurate sub-millisecond spike-based encoding
Composable: Modular design supports hierarchical circuits
Hardware-Compatible: Ported to digital integrate-and-fire cores

Axon SDK Documentation